Simplex/Transformation Animation from INFORMS 2024 Annual Meeting Presentation
In this post, I provide the code for producing the animation above, which momentarily gained popularity on LinkedIn when I used it to promote my presentation Synthesis of Conditional Probability Distributions via Eigenvalue Optimization at the INFORMS 2024 Annual Meeting.
The code is split into two files. The file util.py provides tools that help construct the objects
that are animated, and the file example.py uses those tools to build the animation and write it
to file.
The animation is essentially just a series of
still frames
(
). I initialize the animation by drawing the initial
frame just as I would draw any still figure using matplotlib. I then define a function func
that updates properties of the objects in the figure as a function of the frame, and pass that to
matplotlib.animation.FuncAnimation, which does the real heavy lifting via ffmpeg command-line
tool, one of a handful of “movie writers” that FuncAnimation supports.
from itertools import combinations
import matplotlib.pyplot as plt
import numpy as np
from matplotlib.animation import FuncAnimation
from util import (Si_bbp, colors, get_U, mpl_config, plotsimplex3d, project3d,
rotate3d)
# compute optimal U matrix for given p and q
n = 3
p = np.array([1 / n] * n)
q = np.array([1 / 2, 1 / 3, 1 / 6])
U = get_U(p, q)
# compute identity matrix
I = np.eye(n)
# compute matrix whose rows are all the p vector
O = np.zeros((n, n))
for row in range(n):
O[row, :] = p
# compute initial matrix
r = 0.5
M = r * U + (1 - r) * O
# initialize plot
mpl_config(1)
fig, axes = plt.subplots(1, 2, figsize=(11.5, 7.5), dpi=100)
# draw the solution simplex and the standard simplex
_, _, vertices, edges = plotsimplex3d(M, fig=fig, ax=axes[0])
# redraw lines joining the vertices of the two simplices
lines = {}
for i in range(n):
x, y = project3d([M[i, :], I[i, :]])
lines[i] = axes[0].plot(x, y, '-', color=colors[i], zorder=12)[0]
# draw the barycenter p
x, y = project3d(p)
axes[0].plot(x, y, 'k.')
# annotate the barycenter
x, y = project3d(p + [-0.025, 0.05, -0.025])
axes[0].text(x, y, r'$\boldsymbol{p}$', va='center', ha='center')
# write the trace of the initial matrix solution
tr_text = axes[0].text(0, 0.83,r'$\text{tr}(U) = $' + f'{np.trace(M):2.4f}',
transform=axes[0].transAxes, ha='left', va='top')
# set the size of text objects in axes[0]
for text in axes[0].texts:
text.set_size(16)
# draw the corresponding transformations (in the right plot)
transformations = {}
z = np.linspace(0.00, 1.00, 1001)
for i in range(n):
S = z * 0
for j in range(n):
S += M[i, j] * Si_bbp(z, j + 1, n)
transformations[i] = axes[1].plot(z, S, color=colors[i])[0]
# configure transformation plots, axis limits, axis labels, etc.
axes[1].set_xlim(-0.05, 1.05)
axes[1].set_xlabel('$z$', labelpad=-5, size=16)
axes[1].set_ylim(-0.05, 1.05)
axes[1].set_ylabel('$T_i(z)$', labelpad=-5, size=16)
axes[1].set_xticks([0, 1])
axes[1].set_xticklabels([0, 1], size=16)
axes[1].set_yticks([0, 1])
axes[1].set_yticklabels([0, 1], size=16)
axes[1].axis('square')
# set the position of each subplot
axes[0].set_position((0.05, 0.05, 0.4, 0.9))
axes[1].set_position((0.55, 0.05, 0.4, 0.9))
# define frames to pause in between phases
hold_frames = 20
# define frames in the rotate phases (rotate/pause)
rotate_p1_frames = 180
rotate_frames = rotate_p1_frames + hold_frames
# define frames in the scale phases (expand/hold/shrink/hold/expand/hold)
scale_p1_frames = 60
scale_p2_frames = 180
scale_p3_frames = 120
scale_frames =\
scale_p1_frames + scale_p2_frames + scale_p3_frames + 3 * hold_frames
# define total frames
frames = rotate_frames + scale_frames
# define each angle in the rotate phase
angles = np.concatenate([np.linspace(0, 2 * np.pi, rotate_frames),
np.linspace(0, 0, hold_frames)])
# define each scale in the scale phase
scales = np.concatenate([np.linspace(0.5, 1, scale_p1_frames),
np.linspace(1, 1, hold_frames),
np.linspace(1, -0.5, scale_p2_frames),
np.linspace(-0.5, -0.5, hold_frames),
np.linspace(-0.5, 0.5, scale_p3_frames),
np.linspace(0.5, 0.5, hold_frames)])
# define the function that updates the figure objects
def func(frame, vertices, edges, lines, transformations):
# define base angle and scale
scale, angle = 0.5, 0
# define angle and scale for frames in the rotate phase
beg_frame, end_frame = 0, rotate_frames
if frame in range(beg_frame, end_frame):
scale, angle = 0.5, angles[frame]
# define angle and scale for frames in the scale phase
beg_frame, end_frame = end_frame, end_frame + scale_frames
if frame in range(beg_frame, end_frame):
scale, angle = scales[frame - beg_frame], 0
# update the matrix to reflect the rotation angle and scaling factor
if angle == 0:
M = scale * U + (1 - scale) * O
else:
M = scale * rotate3d(U, np.ones(3), angle) + (1 - scale) * O
# rewrite the matrix trace
tr_text.set_text(r'$\text{tr}(U) = $' + f'{np.trace(M):2.4f}')
# redraw the simplex vertices
for i in range(n):
x, y = project3d(M[i, :])
x, y = [x], [y]
vertices[i].set_xdata(x)
vertices[i].set_ydata(y)
# redraw the simplex edges
for combo in combinations(range(3), r=2):
x, y = project3d(M[combo, :])
x, y = [x], [y]
edges[combo].set_xdata(x)
edges[combo].set_ydata(y)
# redraw lines joining the vertices of the two simplices
for i in range(n):
x, y = project3d([M[i, :], I[i, :]])
lines[i].set_xdata(x)
lines[i].set_ydata(y)
# redraw the corresponding transformations
for i in range(n):
S = z * 0
for j in range(n):
S += M[i, j] * Si_bbp(z, j + 1, n)
transformations[i].set_ydata(S)
return (*vertices.values(),
*edges.values(),
*lines.values(),
*transformations.values())
# fargs are additional positional args to be passed to func
fargs = [vertices, edges, lines, transformations]
# build and write the animation
ani = FuncAnimation(fig=fig, func=func, frames=frames, fargs=fargs, interval=0)
ani.save('animation.gif', writer='ffmpeg', fps=60)from fractions import Fraction
from itertools import combinations
import matplotlib.pyplot as plt
import numpy as np
from matplotlib.cm import tab10
from scipy import stats
from scipy.spatial.transform import Rotation
colors = tab10.colors
C3 = np.array([[0, 0],
[1, 0],
[1 / 2, np.sqrt(3) / 2]])
def mpl_config(scale):
plt.rcParams['font.size'] = 9 * scale
plt.rcParams['font.family'] = 'serif'
plt.rcParams['text.usetex'] = True
plt.rcParams['axes.labelsize'] = 9 * scale
plt.rcParams['axes.titlesize'] = 9 * scale
plt.rcParams['xtick.labelsize'] = 8 * scale
plt.rcParams['ytick.labelsize'] = 8 * scale
plt.rcParams['legend.title_fontsize'] = 9 * scale
plt.rcParams['legend.fontsize'] = 8 * scale
plt.rcParams['mathtext.fontset'] = 'cm'
plt.rc('text', usetex=True)
plt.rc('text.latex', preamble=r'\usepackage{amsmath}')
def project3d(X):
return (X @ C3).T
def rotate3d(X, axis, angle):
axis = axis / np.linalg.norm(axis)
rotation = Rotation.from_rotvec(angle * axis)
return X @ rotation.as_matrix()
def plotsimplex3d(U, fig=None, ax=None):
if fig is None and ax is None:
fig = plt.figure(figsize=(3.5, 3.5), dpi=128)
ax = plt.gca()
I = np.eye(3)
for i in range(3):
x, y = project3d(I[i, :])
ax.plot(x, y, '.', color=colors[i], markeredgecolor='k', markersize=8,
zorder=7)
for combo in combinations(range(3), r=2):
x, y = project3d(I[combo, :])
ax.plot(x, y, '--', color='#000000ff', linewidth=1.5, zorder=5)
vertices = {}
for i in range(3):
x, y = project3d(U[i, :])
vertices[i] = ax.plot(x, y, '.', color=colors[i], markersize=4,
zorder=12)[0]
edges = {}
for combo in combinations(range(3), r=2):
x, y = project3d(U[combo, :])
edges[combo] = ax.plot(x, y, '-', color='#7f7f7fff', linewidth=0.75,
zorder=10)[0]
text_coords = np.array([[ 1.06, -0.03, -0.03],
[-0.03, 1.06, -0.03],
[-0.03, -0.03, 1.06]])
kwargs = {'va': 'center', 'ha': 'center', 'size': 12}
for i in range(3):
kwargs['color'] = colors[i]
ax.text(*project3d(text_coords[i, :]),
f'$\\boldsymbol{{e}}_{i+1}$', **kwargs)
ax.axis('equal')
ax.set_axis_off()
plt.tight_layout()
return fig, ax, vertices, edges
def get_U(p, q):
fraction_bool = all(isinstance(val, Fraction) for val in p)
fraction_bool *= all(isinstance(val, Fraction) for val in q)
n = p.shape[0]
if fraction_bool:
U = np.zeros((n, n), dtype=Fraction)
else:
U = np.zeros((n, n))
for i in range(n):
for j in range(n):
if fraction_bool:
if i == j:
U[i, j] = 1 - max(1 - Fraction(p[i], q[i]), 0)
else:
den = sum(max(p[k] - q[k], 0) for k in range(n))
U[i, j] = Fraction(max(1 - Fraction(p[i], q[i]), 0) *\
max(p[j] - q[j], 0), den)
else:
if i == j:
U[i, j] = 1 - max(1 - p[i] / q[i], 0)
else:
den = sum(max(p[k] - q[k], 0) for k in range(n))
U[i, j] = max(1 - p[i] / q[i], 0) *\
max(p[j] - q[j], 0) / den
return U
def Si_bbp(z, i, n): # based on CDFs of beta distributions
return stats.beta(i, n - i + 1).cdf(z)
You May Also Like
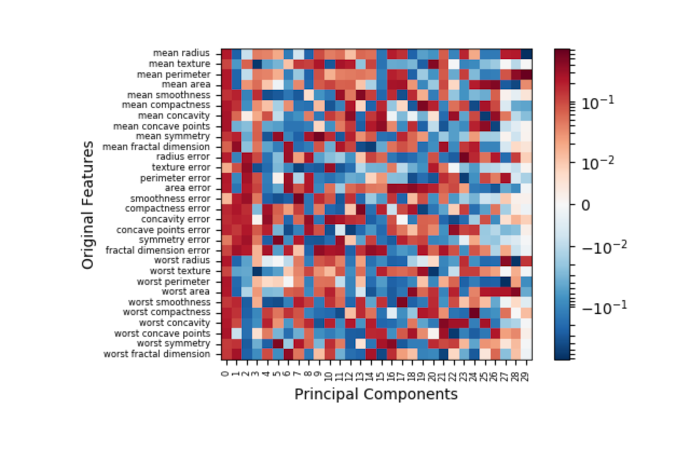
Principal Component Analysis
Recently, I worked on a project that necessitated data exploration and …
The Mixed Integer 0-1 Knapsack Problem
Note: Thanks to Shraddha Ghatkar for pointing out an error in my …
The 0-1 Knapsack Problem, Revisited
When I first started this blog in 2019, one of my first posts was …