I do not have much time or interest for playing Minecraft anymore, but I still boot it up every once in a while just to observe how it has changed since I first played it in 2009. Suffice to say, it has changed considerably! (And so have I!) Last year I started looking into the game mechanics a bit, and I started to realize that virtually everything in the game is subject to structured randomness that affects how tasks like farming may be optimized. In my digging, I encountered this wiki page full of information on game and farming mechanics. However, I suspected that some of the data may be incomplete or flawed, so I took it upon myself to attempt to reproduce the graphic below illustrating the expected number of successful harvests per hour as a function of the harvest frequency.

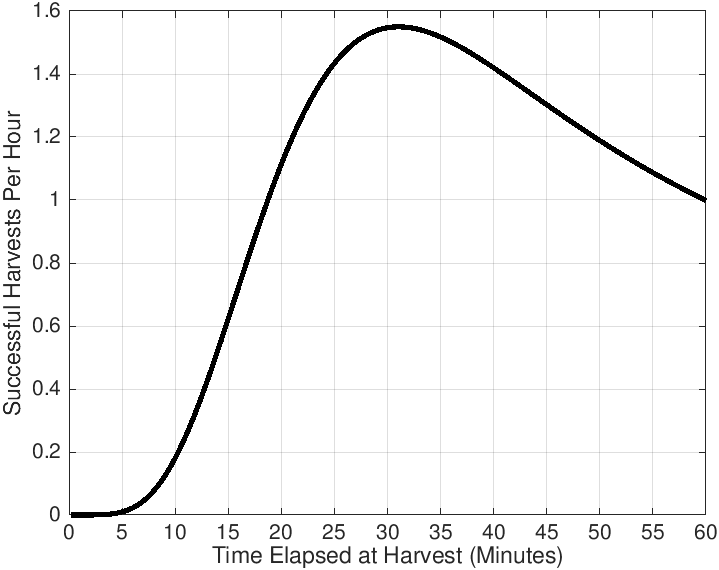
Spoiler: I was able to reproduce this plot, and I am happy to now present the underlying mathematics!

Note: In an earlier revision of this post, I reported that I was unable to perfectly reproduce this plot, which was true at the time. The reason turned out to be that I misunderstood that the first growth stage is reached the instant a seed is planted and not at some random time in the future.

Let’s start by discussing some basics of the game mechanics. Virtually every video game is just a program that runs in a loop. On each cycle of the loop, the game state changes – player input is processed, non-player characters may take actions, events trigger, etc. In Minecraft, a single cycle is referred to as a “tick”. By default, 20 “game ticks” occur each second, and 3 “random ticks” occur once per game tick in each subchunk (a 16x16x16 block area of the map) in the vicinity of the player. A random tick causes a block to update, and block updates are important because they dictate the rate at which crops randomly progress through their various growth stages.

In summary, the probability of a block updating over the course of one game tick is $3 / 4096$. If that block happens to host a planted crop, the probability of the crop growing upon block update is $1 / 3$ under optimal conditions (i.e., sufficient light, ample hydration, and efficient sowing pattern). For more information on these optimal conditions, refer to this section. For our analysis, we suppose that crops are all planted under optimal conditions. As such, the probability of a crop experiencing growth during one game tick is ${p = 3 / 4096 \cdot 1 / 3 = 1 / 4096}.$

Different types of crops must progress through a different number of stages before they may be harvested. For wheat, carrots, and potatoes, there are 8 growth stages. For beetroot, there are only 4. The moment a seed for a crop is planted, the crop enters its first growth stage instantaneously, and the reminaing 3 or 7 growth stages require some random number of ticks to reach. Supposing all crops in a field are harvested together (e.g., by some automated means), our goal is to determine the optimal harvest frequency for 4-stage and 8-stage crops.

First, observe that number of game ticks required for a crop to reach its $k^\text{th}$ stage starting from the first growth stage $k=0$ is distributed according to a negative binomial distribution. For the $k^\text{th}$ stage, the corresponding PMF is

For stages $k=1,2,\ldots,7$, the corresponding PMFs and CDFs for the number of ticks required to reach the stage may be illustrated using a combination of scipy, numpy, and matplotlib:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

import matplotlib.cm as cmap
import matplotlib.pyplot as plt
import numpy as np
import scipy.stats as stats

ticks_per_minute = 1200
time_horizon_minutes = 60
p = 1 / 4096
t = 1 + np.arange(0, time_horizon_minutes * ticks_per_minute)

fig, axes = plt.subplots(2, 1)
for k in range(1, 7 + 1):
    dist = stats.nbinom(k, p)
    color = cmap.viridis.colors[round((k - 1 / 2) * 256 / 7)]
    axes[0].plot(t, dist.pmf(t), color=color)
    axes[0].set_ylabel('$f(t; k, p)$')
    axes[1].plot(t, dist.cdf(t),color=color)
    axes[1].set_xlabel('$t$')
    axes[1].set_ylabel('$F(t; k, p)$')
plt.show()

Though the negative binomial distribution is discrete, we depict it as a continuous distribution due to the enormous size of the sample space over which we plot.

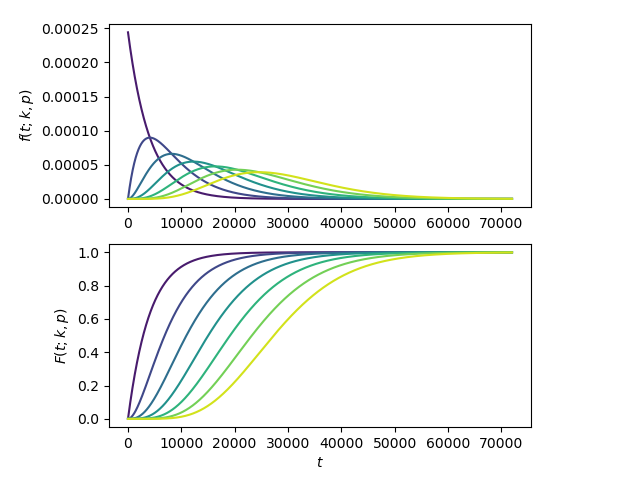
In these plots, stage $k=1$ is represented by the purple line and stage $k=7$ by the yellow. As the growth stage $k$ increases, the corresponding distribution shifts further to the right indicating that more ticks are required to reach a more advanced growth stage. Of course, to obtain the optimal harvest frequency for a crop that must progress through $k+1$ growth stages to be harvested, one need only compute

In the code snippet below, we plot $F(t; k, p)/t$ against $t$ and compute and highlight $t_{k+1}^*$ on the plot for $k=3$ and $k=7$.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

fig, ax = plt.subplots(1, 1)
for k in [3, 7]:
    dist = stats.nbinom(k, p)
    color = cmap.viridis.colors[round((k - 1 / 2) * 256 / 7)]
    ax.plot(t, dist.cdf(t) / t,
            color=color)
    t_star = np.argmax(dist.cdf(t) / t)
    ax.plot(t_star, dist.cdf(t_star) / t_star,
            color=color, marker='.', markersize=10)
    ax.set_xlabel('$t$')
    ax.set_ylabel('$F(t)/t$')
plt.show()

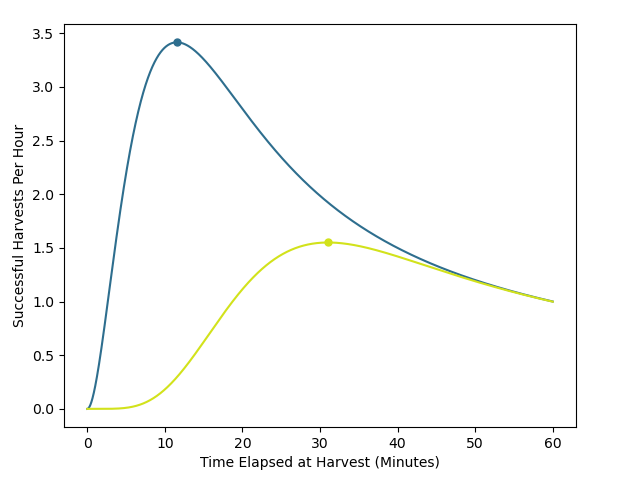
The resulting illustration is shown below.

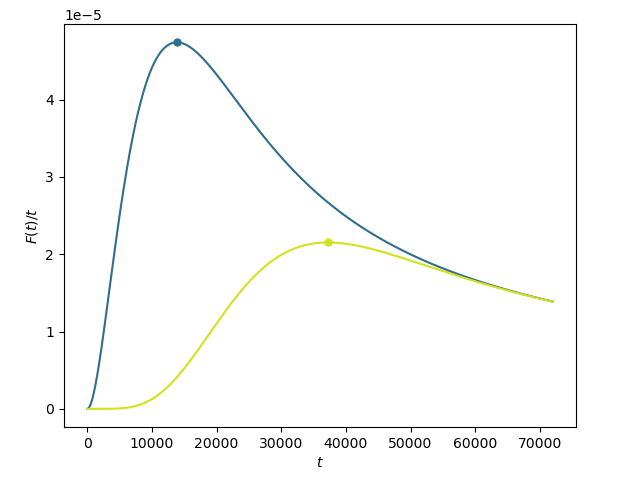
Here, the optimal harvest time $t_4^* = 13853$ ticks shown in blue corresponds to 11.544 minutes in real life. Following this policy, only about $65.70\%$ of crops provide yield on each harvest, and one may expect a rate of $3.415$ successful harvests per crop per hour. The optimal harvest time $t_8^* = 37252$ ticks shown in yellow corresponds to 31.043 minutes in real life. Under this policy, only about $80.19\%$ of crops provide yield on each harvest, and one may expect a rate of $1.550$ successful harvests per crop per hour.

In the figure I attempted to reproduce, the optimal harvest frequency is near to 31 minutes with an expected rate of roughly 1.55 successful harvests per hour, so I am confident that my approach is correct. Finally, I show a version of my plot that normalizes the data to align with the original image.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

minutes_per_hour = 60
fig, ax = plt.subplots(1, 1)
for k in [3, 7]:
    dist = stats.nbinom(k, p)
    color = cmap.viridis.colors[round((k - 1 / 2) * 256 / 7)]
    ax.plot(t / ticks_per_minute,
            dist.cdf(t) / (t / ticks_per_minute / minutes_per_hour),
            color=color)
    t_star = np.argmax(dist.cdf(t) / t)
    ax.plot(t_star / ticks_per_minute,
            dist.cdf(t_star) / (t_star / ticks_per_minute / minutes_per_hour),
            color=color, marker='.', markersize=10)
    ax.set_xlabel('Time Elapsed at Harvest (Minutes)')
    ax.set_ylabel('Successful Harvests Per Hour')
plt.show()

Think I made a mistake? Curious about other features of the game? Let me know in the comments!